Sebelum ke Rumus-Rumus, Contoh Soal dan Pembahasan Bimbel Jakarta Timur menjabarkan definisi secara Matematika, Fisika, Ekonomi dan Rekayasa...
Sebelum ke Rumus-Rumus, Contoh Soal dan Pembahasan Bimbel Jakarta Timur menjabarkan definisi secara Matematika, Fisika, Ekonomi dan Rekayasa
Dalam matematika
Turunan fungsi adalah konsep yang terkait dengan perubahan suatu fungsi terhadap variabel independennya. Dalam istilah yang lebih sederhana, turunan memberikan informasi tentang sejauh mana suatu fungsi berubah ketika nilai variabel independennya berubah. Turunan sering digunakan untuk mengukur kecepatan perubahan suatu fungsi pada suatu titik tertentu.
Interpretasi geometris dari turunan adalah sebagai gradien atau kemiringan garis singgung pada kurva fungsi pada titik tertentu. Turunan memberikan informasi tentang kecepatan perubahan nilai fungsi terhadap perubahan nilai variabel independennya.
Beberapa aturan turunan yang umum digunakan melibatkan aturan pangkat, aturan rantai, dan aturan jumlah/diferensiasi.
Dalam fisika
Turunan fungsi sering digunakan untuk menyatakan hubungan antara berbagai variabel dan untuk mengukur sejauh mana suatu besaran fisika berubah terhadap waktu atau variabel lainnya. Beberapa konsep turunan fungsi yang umum digunakan dalam fisika melibatkan kecepatan, percepatan, dan laju perubahan suatu besaran terhadap besaran lainnya.
Konsep turunan ini memberikan cara matematis untuk menggambarkan perubahan atau laju perubahan dalam berbagai fenomena fisika. Turunan seringkali memainkan peran penting dalam pembentukan persamaan diferensial yang menggambarkan perilaku sistem fisika.
Dalam ekonomi
Turunan fungsi digunakan untuk menyatakan hubungan antara berbagai variabel ekonomi dan untuk mengukur perubahan suatu besaran ekonomi terhadap variabel lainnya. Beberapa contoh penggunaan turunan dalam ekonomi melibatkan konsep elastisitas, produksi, dan utilitas.
Konsep turunan membantu para ekonom untuk memahami respons sistem ekonomi terhadap perubahan dalam variabel-variabel kunci dan mengukur dampak perubahan tersebut pada keputusan ekonomi. Ini memungkinkan ekonom untuk mengambil keputusan yang lebih informasional dan mendalam dalam menganalisis fenomena ekonomi.
Dalam rekayasa
Turunan fungsi sangat penting karena membantu insinyur untuk memahami dan mengoptimalkan berbagai fenomena fisika atau matematika yang muncul dalam perancangan dan analisis sistem rekayasa. Beberapa aplikasi turunan dalam rekayasa melibatkan analisis sinyal, kontrol sistem, optimisasi, dan permodelan sistem fisik. Berikut adalah beberapa contoh penggunaan turunan dalam rekayasa:
1. Analisis Sinyal (Signal Analysis):
- Dalam pemrosesan sinyal, turunan sering digunakan untuk menganalisis karakteristik sinyal. Turunan sinyal dapat memberikan informasi tentang frekuensi, amplitudo, dan fase.
2. Kontrol Sistem (Control Systems):
- Dalam analisis dan desain sistem kontrol, turunan sering digunakan untuk mengukur laju perubahan suatu variabel terhadap waktu. Misalnya, turunan posisi terhadap waktu memberikan kecepatan, dan turunan kecepatan memberikan percepatan.
3. Optimisasi (Optimization):
- Dalam masalah optimisasi, turunan digunakan untuk menemukan nilai minimum atau maksimum suatu fungsi. Turunan pertama dan kedua sering digunakan dalam analisis titik stasioner (titik kritis) untuk menentukan apakah suatu solusi merupakan minimum, maksimum, atau titik saddle.
4. Permodelan Dinamis Sistem Fisik:
- Turunan berperan penting dalam permodelan matematis sistem fisik yang dinamis, seperti persamaan gerak dalam mekanika atau hukum-hukum dasar elektronika.
5. Pemrosesan Citra (Image Processing):
- Dalam pemrosesan citra, turunan dapat digunakan untuk mendeteksi tepi atau perubahan intensitas dalam citra.
6. Analisis Struktur (Structural Analysis):
- Dalam analisis struktur, turunan digunakan untuk menghitung momen, tegangan, dan deformasi dalam elemen struktural. Turunan juga digunakan dalam permodelan respons dinamis struktur terhadap beban dinamis.
7. Analisis Perpindahan Panas (Heat Transfer Analysis):
- Dalam analisis perpindahan panas, turunan digunakan untuk menghitung gradien suhu dan menggambarkan distribusi panas dalam suatu sistem.
8. Analisis Sistem Elektromagnetik:
- Dalam analisis sistem elektromagnetik, turunan digunakan untuk memodelkan hubungan antara medan elektromagnetik dan sirkuit listrik.
Turunan juga terlibat dalam pembuatan model matematis sistem dan memainkan peran penting dalam analisis numerik untuk memecahkan persamaan diferensial dan permasalahan matematika lainnya yang muncul dalam rekayasa. Oleh karena itu, pemahaman yang kuat tentang konsep turunan sangat penting bagi insinyur rekayasa.
y adalah fungsi dari x atau y=f(x), turunan fungsi dinotasikan sebagai y' atau f ‘(x) atau dy/dx
Maka turunan fungsi y=f(x) terhadap x didefinisikan sebagai :
A. Definisi
Untuk y adalah fungsi dari x atau y=f(x), turunan fungsi dinotasikan sebagai y' atau f ‘(x) atau dy/dx
Maka turunan fungsi y=f(x) terhadap x didefinisikan sebagai :
Contoh :
Jika f (x)=x2 – 3x, maka turunan fungsi f (x)adalah
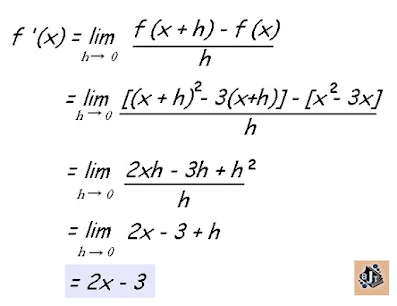 |
| Rumus 2 |
B. Rumus Dasar Turunan
- · Turunan fungsi konstan k. Jika f(x)=k, maka f ‘(x)=0
- · Jika f(x)=ax, maka f ‘(x)=a
- · Jika f(x)=axn, maka f ‘(x)=anxn-1
- · Jika f(x)=u(x) + v(x), maka f ‘(x)=u’(x) + v’(x)
- · Jika f(x)=u(x) . v(x), maka f ‘(x)=u’(x) .v(x) + v’(x) . u(x)
v(x)
maka f ‘(x)= u’(x) . v(x) + v’(x) . u(x)
[v(x)]²
· 7. Jika f(x)=[u(x)]n, maka f‘(x)=n [u(x)]n-1.u’(x)
· 8. Turunan fungsi komposisi (dalil rantai)
Jika y=f(g(x)), maka =dy = dy .dg
dx dg dx
TURUNAN FUNGSI TRIGONOMETRI
- Jika f(x)=sin x, maka f’(x)=cos x
- Jika f(x)=cos x, maka f’(x)=-sin x
- Jika f(x)=tan x, maka f’(x)=sec2x
PERSAMAAN GARIS SINGGUNG DAN GARIS NORMAL KURVA
- · Gradien garis singgung kurva di titik (x1,y1)pada kurva f(x) adalah m=f’(x1)
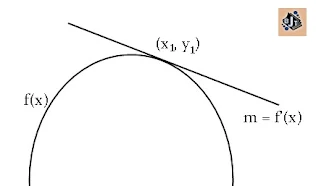 |
| Gradien |
Persamaan garis singgung kurva
y – y1=m (x – x1)
·
- Garis normal kurva adalah suatu garis yang tegaklurus dengan garis singgung kurva di titik yang sama dengan titik singgungkurva.
 |
| Kurva |
· Gradiengaris normal kurva di titik (x1,y1) pada kurva f(x)
a adalah mn=-1/f'(x)
· Persamaan garis normal kurva
y – y1=mn (x – x1)
FUNGSI NAIK, FUNGSI TURUN DAN NILAI STASIONER
- · Fungsi naik
Suatu fungsi dikatakan naik dalam suatuselang untuk x1 < x2 maka f(x1) < f(x2)
kurva naik jika f’(x) > 0
- · Fungsi turun
Suatu fungsi dikatakan turun dalam suatuselang untuk x1 < x2 maka f(x1) > f(x2)
kurva naik jika f’(x) < 0
- · Nilai dan titik stasioner
Jika fungsi f(x) mempunyai turunan pada x=a dan f’(a)=0, maka f(a) merupakan nilai stasioner fungsi f(x)
Jika f’(a)=0, maka titik stasioner fungsiadalah (a, f(a))
· Jenis nilai stasioner dimana f”(x) adalahturunan kedua fungsi f(x)
Jika f”(a) < 0, maka f(a) berjenismaksimum
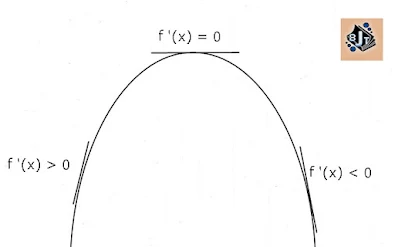 |
| Kurva 2 |
Jika f”(a) > 0, maka f(a) berjenis minimum
 |
| Kurva 3 |
Jika f”(a)= 0, maka (a, f(a)) adalah titik belok
 |
| Kurva 4 |
CONTOH SOAL DAN PEMBAHASAN
1. Turunan pertama dari fungsi f(x)=4x3 -3x2 + 8x -5 adalah….
Pembahasan:
f’(x) =4.3.x3-1 – 3.2.x2-1+ 8.1 x1-1 -5.0.x0-1
=12x2 – 6x1 + 8x0 – 0
=12x2 – 6x + 8
Pembahasan:
misal u(x)=3x2 +2, u’(x)=6x
v(x)=2x -5, v’(x)=2
maka y’=u’(x) . v(x) + v’(x) . u(x)
=6x (2x – 5) + 2 (3x2+2)
=12x2 – 30 x + 6 x2+ 4
=18x2 – 30x + 4
3. Turunan pertama dari dari y=(5x2 +3 x)3adalah…
Pembahasan:
misal u(x)=(5x2 +3x), u’(x)=10x + 3
y=[u(x)]n, maka y' =n [u(x)]n-1.u’(x)
= 3(5x2 +3x)2(10x + 3)
= (30x + 9)(5x2 +3x)2
1. 4. Turunan pertama dari fungsi y=∛(6x+5) adalah…
Pembahasan:
y=(6x + 5)1/3,u(x)=6x=5, u’(x)=6
y’=1/3 (6x + 5)-2/3(6)
=2(6x + 5)-2/3
= 2
∛(6x+5)²
5. Turunan pertama dari fungsi f(x)=3x + 2 adalah…
x - 1
Pembahasan:
u(x)=3x+2, u’(x)=3
v(x)=x-1, v’(x)=1
maka f ‘(x)= u’(x) . v(x) - v’(x) . u(x)
[v(x)]²
=3(x-1) - 1(3x+2)
(x-1)²
= -5
(x-1)²
6. Persamaan garis singgung para bola y=x2+ 4x -5
pada titik (-1,2) adalah…
Pembahasan:
y’=2x + 4
m=2(-1) + 4=2
persamaan garis singgung
y – 2=2 (x –(-1))
y – 2=2x + 2
y=2x + 4
2 7. Persamaan garis normal kurva y=x3-4x2+ 5x-2
pada titik (2,-5) adalah…
Pembahasan:
y’=3x2- 8x + 5=3(2)2– 8(2) + 5=1
mn=-1/y’=-1/1=-1
persamaan garis normal
y – (-5)=-1(x-2)
y + 5=-x + 2
y=-x -7
8. 8. Fungsi f(x)=x2 – 9x naik pada interval…
Pembahasan:
fungsi naik jika f’(x) > 0 ,
maka 2x –9 > 0
jadi fungsi naik pada x > 4,5
9. 9. Tentukan nilai stasioner dari fungsi f(x)=2x3 – 15x2 +36x – 10 !
Pembahasan:
titik stasioner dicapai jika f’(x)=0
6x2 -30x + 36=0
6 (x -2) (x-3)=0
x1=2, x2=3
Nilai stasioner didapat
f(2)=18 dan
f(3)=17
10. Tentukan turunan pertama dari y=sin³(2x+3)
Pembahasan :
y'=3sin²(2x+3).cos(2x+3) (2)
=6sin²(2x+3).cos(2x+3)

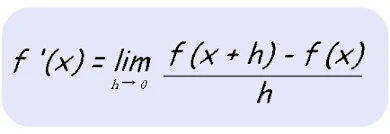





Tidak ada komentar